Probabilistic Data Structures

Suppose let’s say you are signing up for the new Email id. When you enter a new mail id, respective mail service will check whether the given mail id already exists.

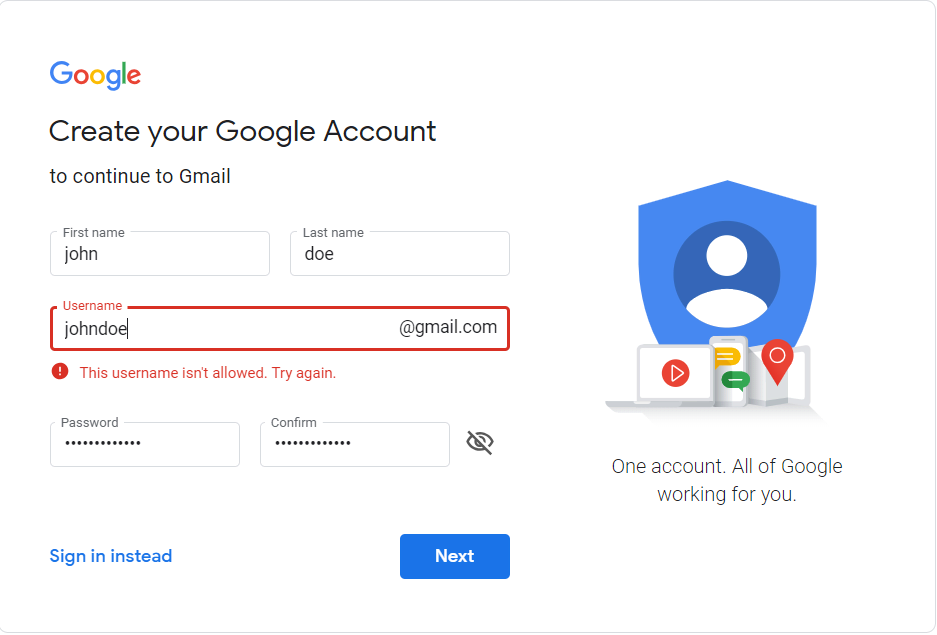
So how can we build such a kind of systems ? Think for a minute before continue reading

• Keep all email id’s in memory i.e. Cache, It’s not practical to keep all email id’s in memory.
• Store it in database/disk and check whether the given email id exist by reading or querying from db/disk. This will be more time consuming.

Let’s see how we can use probability data structures to build these kind of system

Table of contents

Bloom Filter

It is a space-efficient probabilistic data structure for representing a set D = {x1, x2,…, xn} of n elements that supports only two operations.

• Adding an elements to the set {Add}
• Checking whether the element exist in the set or not {Contains}

When bloom filter checks whether an item exist in the set, it can give either it’s present or not present. If the bloom filter gives the result as not present, it’s 100% sure the item does not exist in the set but it is not same for when the result is present, because when the result is present, it’s only 90% sure that the item exist.

- Contains(item) => “May be in the set” or “Definitely not in set”
- Definitely not in set is 100%

Hashing plays the central role in probabilistic data structures as they use it for randomization and compact representation of the data.

So, what is hashing ?

Hashing is a function which takes an inputs of varying size and generates fixed size value which is called hash value.

There are many hash functions available, the choice of hash function are important to avoid bias. When a hash function compresses the input, it may generate same hash value for two or more different inputs which is unavoidable and this is called hash collision. Probabilistic data structures uses non-cryptographic hash functions. The reason for the use of non-cryptographic hash function is that they’re significantly faster than cryptographic hash functions.

The bloom filter is represented by a bit array and can be described by its length L and number of different hash functions H. Each hash function should be independent and uniformly distributed. In this way, we randomize the hash values uniformly (you can think of it as using hash functions as some kind of random-number generator) in the filter and decrease the probability of hash collisions. Such an approach drastically reduces the storage space and, regardless of the number of elements in the data structure and their size, requires a constant number of bits by reserving a few bits per element.

In the beginning the bit array of length L all bits are equal to zero. i.e. Set is empty.

To insert an element x into the filter, for every hash function H(i) we compute its value j = H(i){x} on the element x and set the corresponding bit j in the filter to one. Note, it is possible that some bits can be set multiple times due to hash collisions.

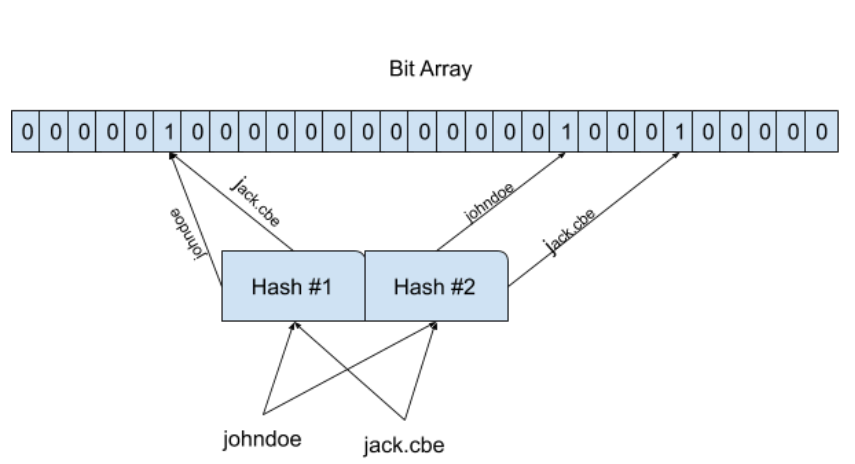In the above diagram, I’ve used only two hash function, but in practice, we will use more hash functions. It is possible that different elements can share corresponding bits(both inputs shared 5th index in the above pic).

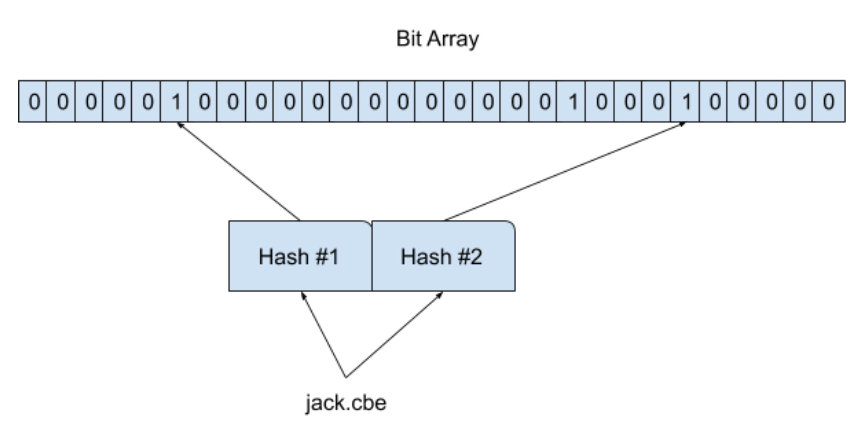
When we check for the element x in the filter, we compute all hash functions H(i){x} for i=1,2,…n and check bits in the corresponding positions. If all bits are set to one, then the element x may exist in the filter. Otherwise, the element x is definitely not in the filter.

In the above case, for the input “justincampell” we compute all hash functions in this case we have two hash functions and that gives us two indices(2, 8). Thus, checking the bits 2 and 8, we see that bit 2 isn’t set, therefore the item “justincampell” is definitely not in the set and we don’t even need to check bit 8.

Code

• Let’s define bloom filter struct in go

// BloomFilter struct definition
type BloomFilter struct {
	bitArray      []bool        // BloomFilter bit array
	bitArraySize  int           // Number of bits to use to persist elements
	maxSize       int           // Maximum Size of the bloom filter
	hashFunctions []hash.Hash64 // List of hash functions
}

• Adding an element to the set

// Add adding an elements to the filter
func (bl *BloomFilter) Add(item []byte) {
	indices := bl.fetchIndices(item)
	for _, index := range indices {
		bl.bitArray[index] = true
	}
}

• Checking whether the element exist in the set or not

func (bl *BloomFilter) Contains(item []byte) bool {
	indices := bl.fetchIndices(item)
	for _, index := range indices {
		bitValue := bl.bitArray[index]
		if !bitValue {
			return false
		}
	}
	return true
}

Complete code in github

Use Cases

• Google Bigtable, Apache HBase and Apache Cassandra, Postgresql and many more databases use Probabilistic data structures to reduce the disk lookups for non-existent rows or columns. Avoiding costly disk lookups considerably increases the performance of a database query operation.

• Medium uses Probabilistic data structures to check if an article has already been recommended to an user.

• Ethereum uses Probabilistic data structures for quickly finding logs on the Ethereum blockchain.

• URL Shortners

• The Google Chrome web browser used to use a Probabilistic data structure to identify malicious URLs.

• For realtime monitoring dashboards and many more.

Conclusion

• Probabilistic data structure is a data structure which always provides approximated answers, but with reliable ways to estimate possible errors.

• False positive is possible but false negatives are not. False Positive, Item does not exist but bloom filter says it does. False Negative, Item do exist but bloom filter says it does not.

References